Numerical method
The scientific question at hand decides what numerical method is the best to search for answers. Hence in our group, we develop and run various numerical methods and -simulations, use high performance computing, and combine different computational techniques in our research.
Hydrodynamical Simulations
We are the main developers of the JUPITER hydrodynamical code since 2015. This is a three dimensional Godunov code that solves the basic hydrodynamical equations combined with radiative transfer. It has various rotatinf and non-rotating coordinate systems implemented (Cartesian, Cylindrical, Spherical) with nested meshing that allows increasing the resultion within the simulation box. JUPITER has multi-fluid capabilities, hence e.g. gas+dust simulations can be carried out.
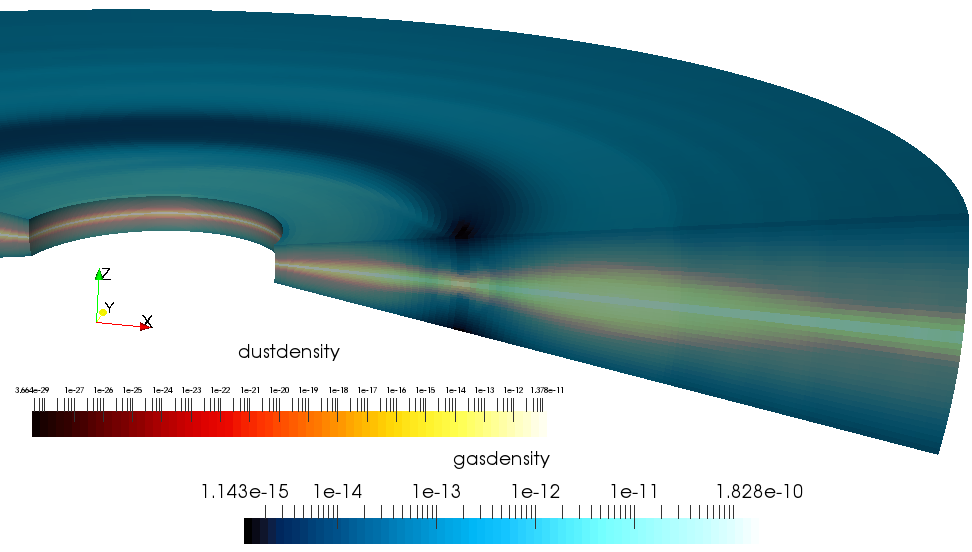
Radiative Transfer
In astrophysics, propagation of radiation though matter is solved through radiative transfer. We use various radiative transfer techniques as a stand-alone, or as an incorporated module in our computations. We developed radiative transfer intro our hydrodynamical code, which allows us to get a high precision on calculating temperature. Radiative transfer tools are also used by us in a post-processing step, when we crate predictions for observations from our simulations.
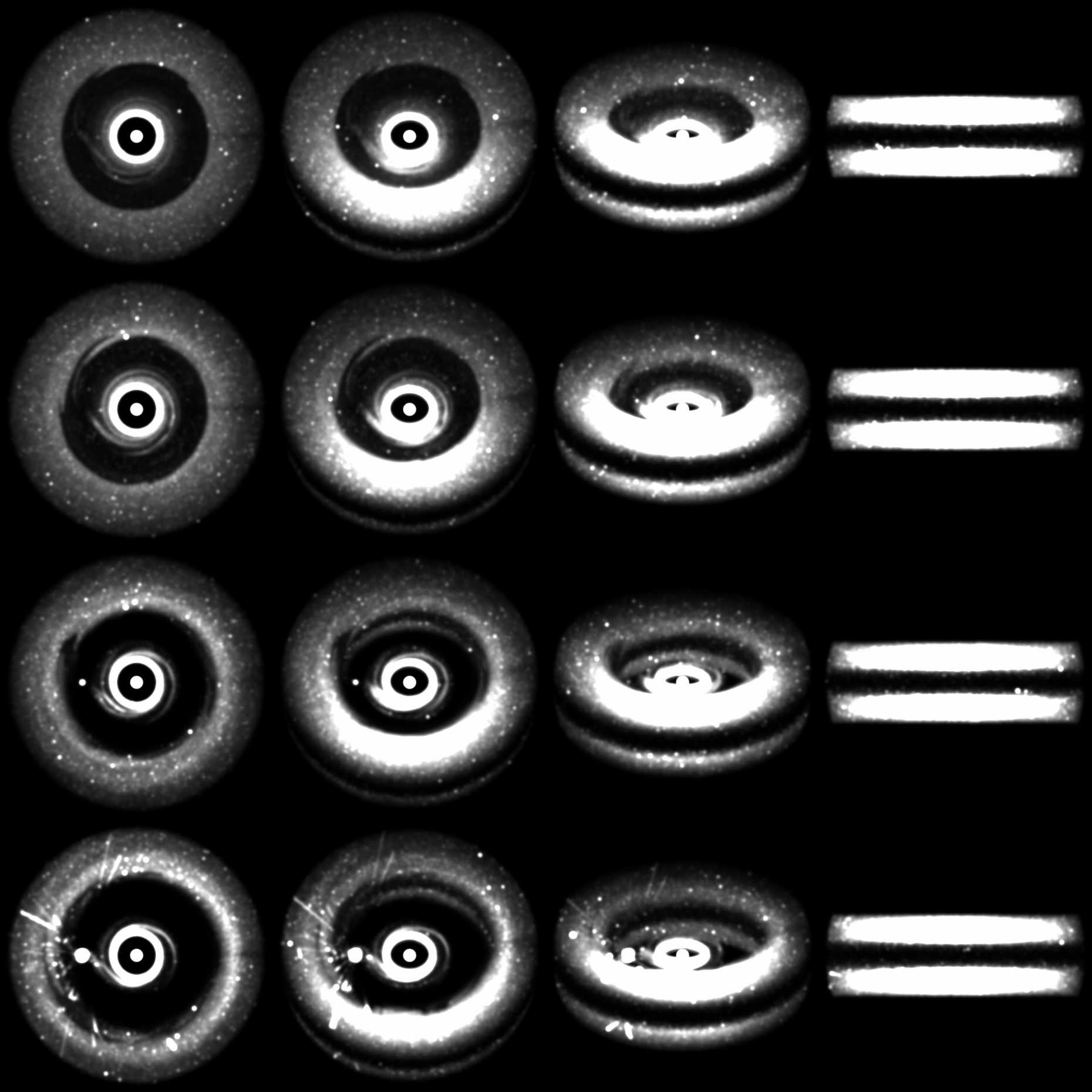
N-body simulations
N-body gravitational solvers are widely used in astrophysics. In this technique we have numerous mass points, that interact with each other via their gravity. E.g. when we are interested in the long-term stability of a planetary system, we have N-bodies (the planets) whose dynamical evolution we can follow with N-body simulations. Another example is when we study rocky planet (or moon) formation, we have numerous smaller building blocks whose collisions will eventually build up the planets/moons.
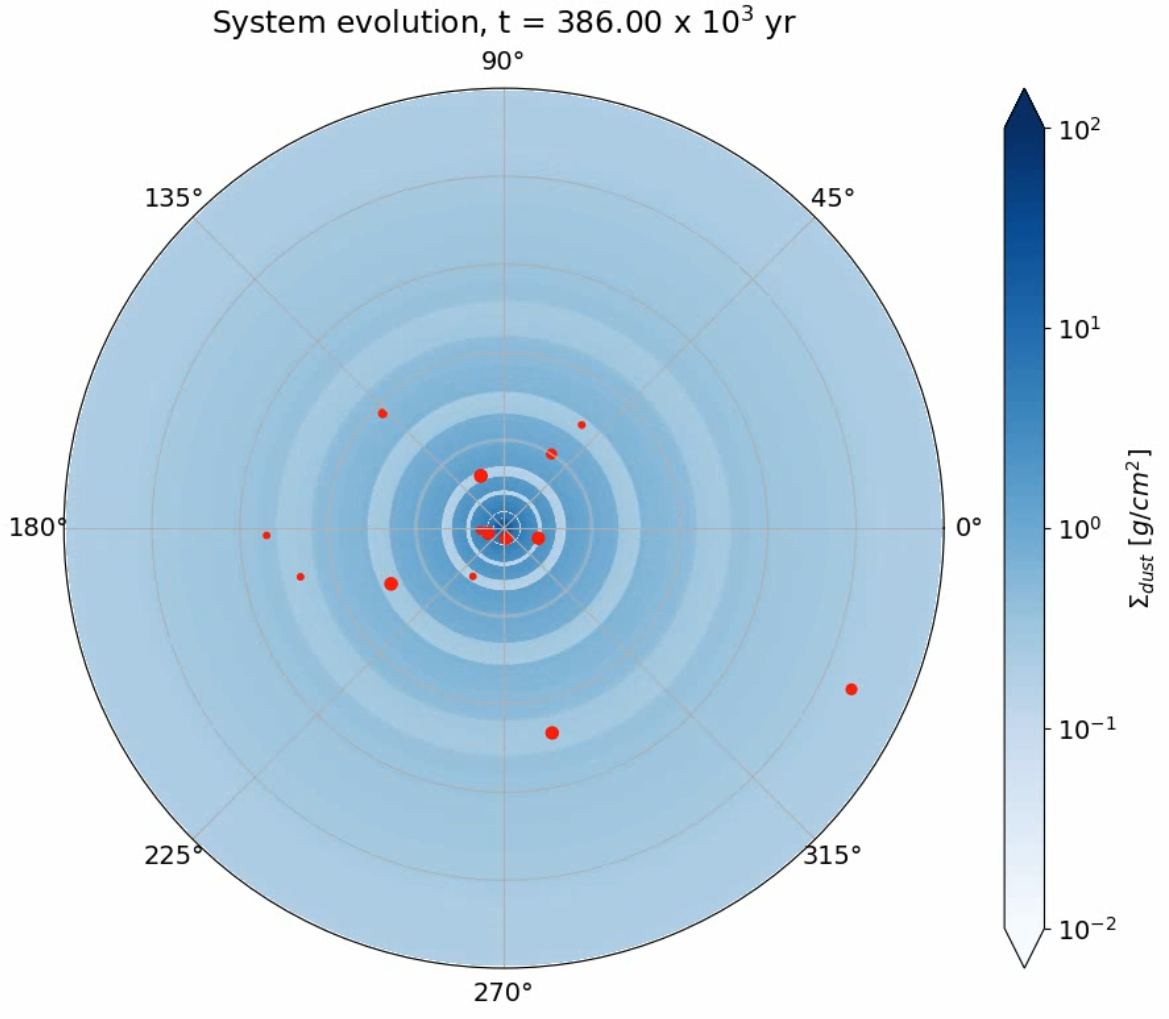
Population Synthesis
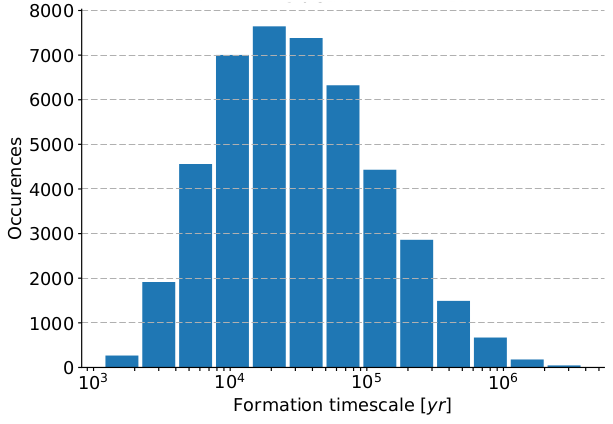
This method we use a series of phenomenological partial differential equations that we solve together to create various outcomes of randomized initial parameters. For example, depending on the initial distribution of the building blocks of planets, we get out different planetary system in each case. Varying a few initial conditions within a range that is scientifically justified, and running hundred of thousands of individual simulations, we get out a population of the resulting systems, that we can statistically analyze, e.g. by creating histograms of the planet formation timescale, the mass of planets, and their orbital parameters. Population synthesis uses various partial differential equation solvers, semi-analytical methods and different statistical methods to solve and analyze astrophysical questions at hand.
Machine Learning
Various machine learning techniques are used in astrophysics to help with data analysis. In our group, we also increasingly use various machine learning methods to help our analysis, to speed up computational times. While this is not our main technique for our research, we use it when necessary or when it increases performance.